A Challenge of Using Harmonic Mean as a Calculation of Space Mean Speed on a Fixed-segment: Proof of

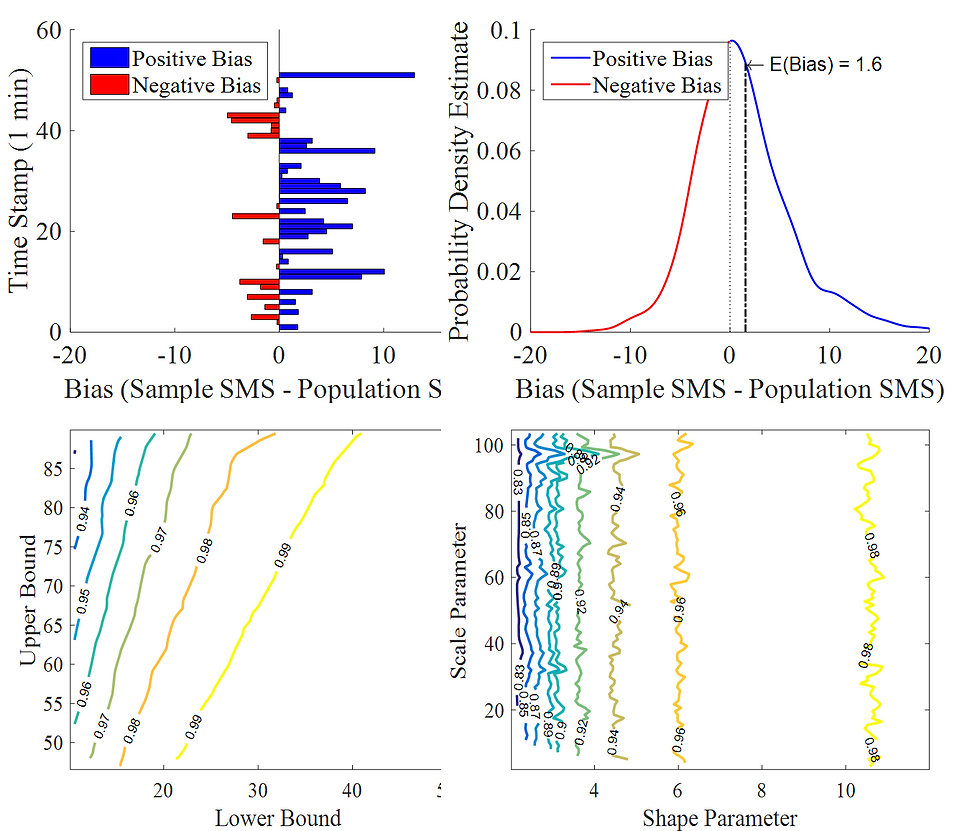
Harmonic mean, which is the reciprocal of the arithmetic mean of the reciprocals of observations, is considered to be an appropriate average for rates or ratios. In transportation, the harmonic mean is used to calculate Space Mean Speed, where a designated segment length is fixed or passing vehicles are assumed to complete the segment with given speeds. This study identifies and proves a sampling bias of harmonic mean, which definitively affects the sampling bias of the space mean speed on the fixed segments. The study shows, a mathematical proof and numerical example, that harmonic mean is overestimated when the sample size is smaller than the population. The study also provides both analytical and simulation-based correction approach. From the simulations and the three case studies of investigating the impact of the sampling bias in this study, it is recognized that the sampling bias is affected by sampling rate, time interval, segment length, and distribution type.